3N 航海筆記試験問題沿岸航法（クロス方位法）

以下は，三級海技士（航海）の筆記試験における，沿岸航法に関する過去問題です。よく出る問題です。
※ 出題は，平成20年7月から平成30年2月定期試験までの問題を調べたものです。「平成/年」を数字で示しております。

問題

沿岸航行中，2つの物体を用い，クロス方位法で船位を求める場合，方位線はどのような交角になるのがよいか。理由とともに述べよ。

【出題：22/07,25/07,27/07,28/04,29/07】

答えから言いますと，クロス方位法の方位角の交角θ（2物標による場合），θ＝90°となる場合が方位線が最も良くなります。このため，少なくとも30°≦θ≦150°の範囲となるようにする必要があります。

理由は，方位誤差による船位の誤差が，sinθに反比例するためで，θ＝90°のときsin90°が1となることから，誤差が最小となります。したがって，θ＝90°となるような物標を選ぶことにより誤差を小さくすることができるのです。

まあ，ここまでは，三級の解答なのですが，実際，どのように誤差を求めるかが，二級海技士（航海）筆記試験の問題にあります。

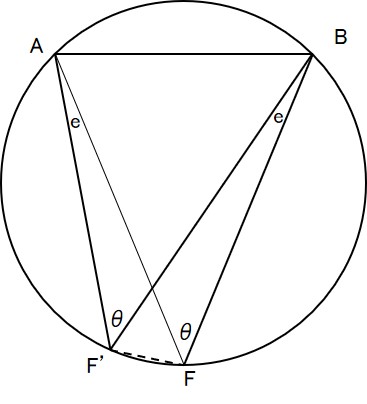
下図において、A，Bを2つの灯台の位置とし、Fを真の船位，F’を方位誤差（e）を含んだ船位，θは両物標の方位の差とすると、船位の誤差はFF’となります。

△ABFにおいて

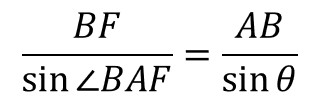・・・①

△BFF’において

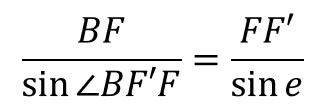・・・②

A，B，F，F’は同一円周上にあるので、円周角の法則から，

∠BAF＝∠BF’F・・・③

①②③より、

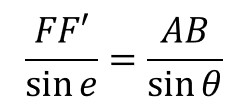
したがって，

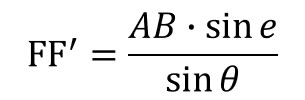
となり，誤差（FF’）は，sinθと反比例することになります。

二級海技士（航海）筆記試験では，この式を求めた後，灯台間の距離（AB）と方位誤差（e）を代入して，誤差（FF’）を求めます。