レーダーによる船位を求める問題ですね。これは，レーダーの誤差がどの程度かを覚えておく必要があります。まず，レーダーで方位を測るのと，距離を測るのと，どちらが誤差が少ないのでしょうか？これは，忘れてはいけません。距離の方が，方位よりも誤差が少ない！！レーダーによる方位測定には約2度の誤差があります。一方の距離測定の場合は，誤差約2％です。ちなみに視覚によるコンパス方位の誤差は，1%以内程度です。えっ，レーダーの方位の誤差が2度だったら，360分の2で180分の1じゃん，1%未満じゃん，ですって。2度は，角度の誤差であって，遠くになるほど，2度でも距離の誤差が大きくなりますよね。そういうことです。2度の誤差は，一概に%で誤差（測位誤差）を示すことが出来ないのです。そのようなことを踏まえると，測位誤差の少ない順番は，自然に導かれますね。
一方で，遠い物標を使用してレーダー測位を行う場合は，地球が丸いことに注意する必要があります。
レーダーの画面上の近くの物標と遠くの物標がどのように映るかよく考えて答えましょう。

そうですね。まずは，本当に予定の変針点にあとどのくらいで到達するか確認をしなければなりませんね。
つまり，船位の確認（コースラインからどれだけずれているかも含む）ですね。
次に，このまま変針しても良いか，周囲の状況を確認する必要がありますね。
そして，どの変針目標をどのように見て（予備の変針目標も含む），どのような方向に変針するか（これは変針点に達する前に事前に覚えておく必要があります）再確認します。
さらに，変針を行うために，舵を手動操舵に切り替えなければなりませんね。
これらのことを流れで覚えて，箇条書きで答えられるようになりましょう。

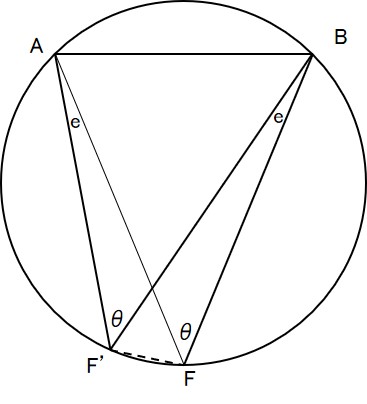
クロス方位法の方位角の交角θ：2物標による場合，θ＝90°となる場合が最も良い。少なくとも30°≦θ≦150°の範囲となるようにする。

理由：方位誤差による船位誤差はsinθに反比例するため，θ＝90°のとき（sin90°＝1）に誤差が最小となる。したがって，θ＝90°となるような物標を選ぶことにより誤差を小さくすることができる。

図において、A，Bを2つの灯台の位置とし、Fを真の船位，F’を方位誤差（e）を含んだ船位，θは両物標の方位の差とすると、船位の誤差はFF’となります。
△ABFにおいて
BF/sin(∠BAF) =AB/sin⁡θ    ・・・①   △BFF’において      BF/sin⁡(∠BF′F) =FF′/sin⁡ e ・・・②
A，B，F，F’は同一円周上にあるので、円周角の法則から、        ∠BAF＝∠BF’F・・・③      ①②③より、   FF′/sin⁡ e =AB/sin⁡θ     ゆえに、FF′=(AB∙sin⁡e)/sin⁡θ  
ここで、e（方位誤差）=2°，AB（両灯台の距離）=11マイル，θ（両物標の方位差）=70°を代入すれば、
FF′=(11・sin2°)/sin⁡55°=0.4686      答：0.5マイル