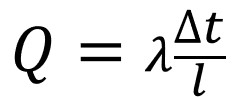円の面積を求める公式

おはようございます。

本日は，円の面積を求める公式についてお話しましょう。

えっ，そんなこと分かっているから，話さなくていいですって。

まあまあ，たまには，こんな話もいいじゃないですか。

という訳で，少しだけお付き合いください。

さて，小学生の時に円の面積を求める公式を習いましたね（たぶん）。

円周率は分かりますよね。時代によって，円周率（）が「3」だったりするようですね。私の場合，小学生の時に円周率は，3.14と習った世代です。

基本的に，海技試験や実務においては，関数電卓にがあるので，覚えなくても良いし，桁数も多いので正確な計算が出来ます。

さて，それ以外にもを使用する利点があります。

それは，計算問題を解く場合です。

それと，円の面積を求める場合，直径（d）と半径（r）の使い分けも重要となります。

海技試験の計算問題の場合，直径と半径がどちらが多いか？

圧倒的に直径が多いのでは，ないのでしょうか？

このため，計算問題を解く場合，直径を直接記号として当てはめる必要があります。

小学生の頃の円の面積を求める公式は，半径×半径×円周率という表現でなかったでしょうか。

これを，直径で示す式にするとどうなるでしょう。

下図のように直径は，半径が2つ分ですから，半径を直径で表そうとすると2分の１ですね。

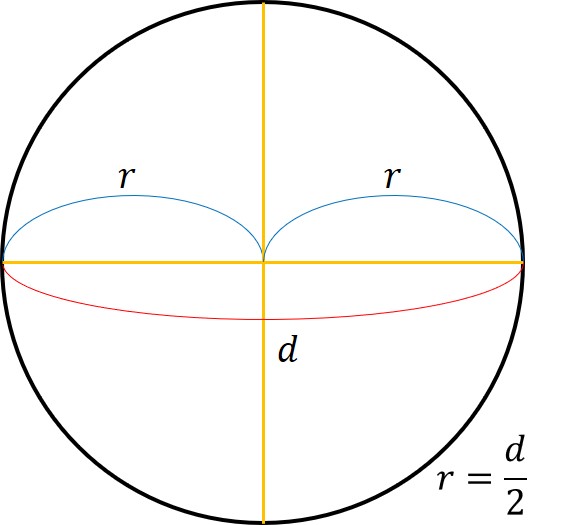
ということは，円の面積（A）を求める式を直径で表すと

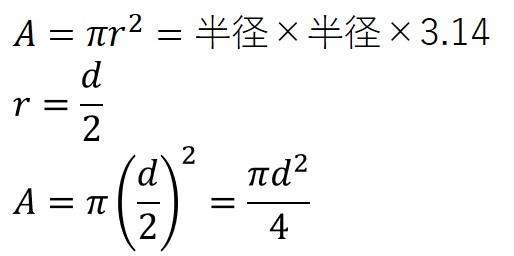
ですね。

これを踏まえ，パイプの断面積を求める公式を求めてみましょう。

外径を，内径をとすると（ｔはパイプの厚み），

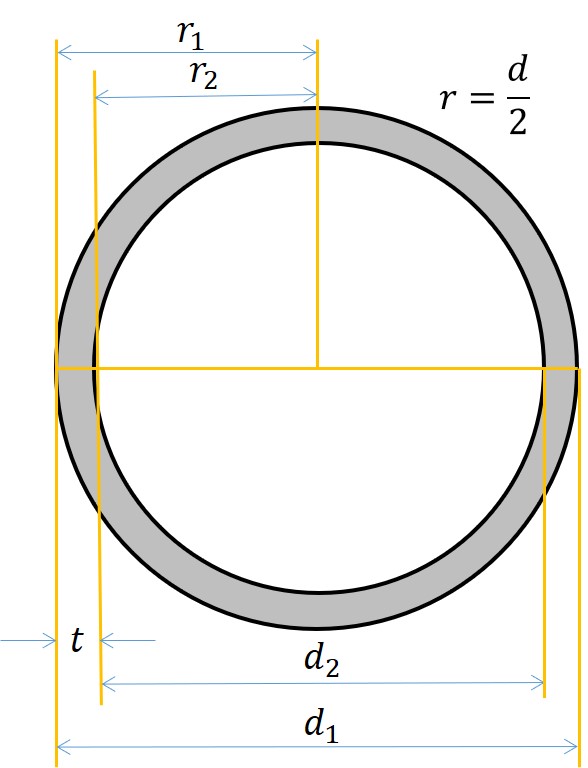
となるので，式ですと，

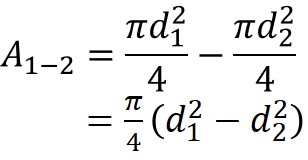
となります。

ちなみに，外径とパイプの厚みが示されている場合に，パイプの断面積を求める式は，

となります。

記号を使用し，整理した上で，数値を代入するようにすれば，電卓を打つ回数も減り，間違える可能性も減ります。

このため，計算問題では，まず略図を描き（記号で示し），式を整理し，最後に数値を代入して計算し，答えを求めましょう。